İnternette Fotoğraf Paylaşmanızı Sağlayan 200 Yıllık Formül

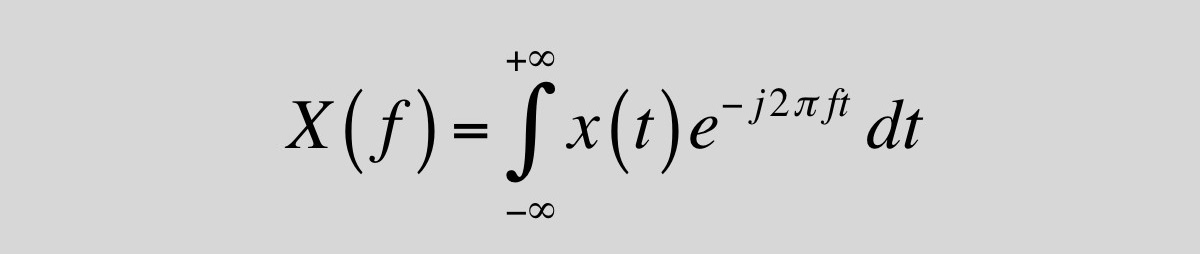
Sakin olun.

Burada gördüğünüz formül neredeyse 2 asırlık ancak bugün onun sayesinde birtakım kullanışlı teknolojilere sahibiz. İstediğimiz müziğe saniyeler içerisinde ulaşıyor, istediğimiz manzarayı anında çevre medyada paylaşabiliyoruz. 

Tüm bunların matematikle ne kadar ilgisi olduğuna karşılık arıyorsunuz, biliyoruz. Bunun için bilincimizdeki devir makinesine biniyor ve 1822 yılına, Fransa’daki bir kütüphanede gözümüzü açıyoruz. Raflarda duran yeni basılmış 'Isının Analitik Teorisi' isimli bir kitap dikkatimizi çekiyor. Sahifelerini çeviriyor, tıpkı formülü tekrar önümüzde görüyoruz. 

Kitabı muharririne bakıyoruz: Baron Jean-Baptiste-Joseph Fourier

9 yaşında ana ve pederini kaybedince büyük bir darbe yedi, askeri mektepte aldığı eğitimle içindeki matematik dehasını ortaya çıkardı. Fourier, yukarıdaki formülü ortaya koyan matematikçiydi.Ancak yaptığı şeyin gelecekteki kişilerin hayatlarını nasıl değiştireceğinden bihaberdi. 

Fourier’in yaptığı matematiğin hudutlarını aştı, mühendislik ve teknolojiye önemli halde istikamet verdi.

Pekala, bu dâhi aslında neyin peşindeydi?


Fourier, aslında ısının nasıl iletildiğiyle ilgileniyordu. Onun merakı, bu tuhaf kuvvetin unsurların içinde ne süratte ve nasıl ilerlediği üzerineydi. Yaptığı çalışmalarla bir formül geliştirdi.

Bugün elektromanyetik sinyal dediğinizde aklınızda bu türlü frekans dalgaları beliriyor mu?


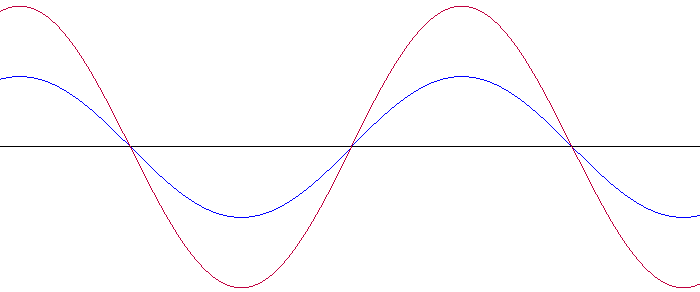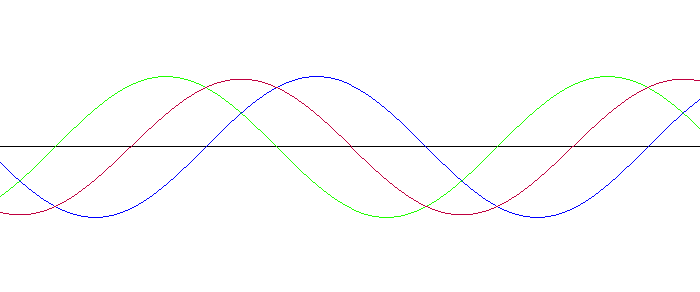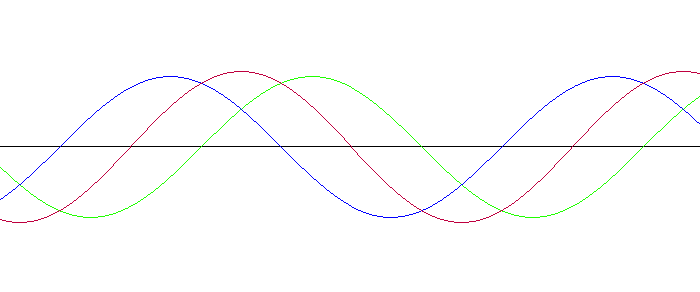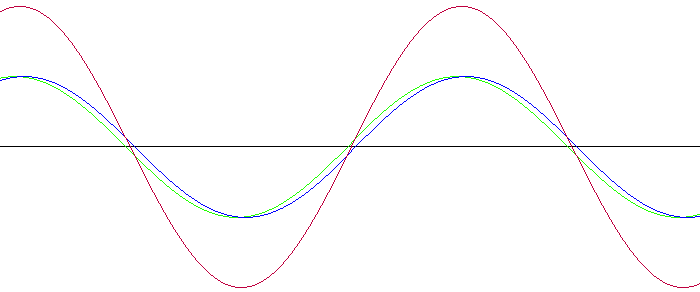
Fourier, daha elektromanyetik sinyalleri görselleştiremediğimiz yıllarda, tuhaf bir ilişkiyi keşfetmişti. Karmaşık frekansa sahip sinyallerin, tertipli frekansa sahip sinyallerin birleşiminden oluştuğunu anladı. Yani birden ziyade kolay sinyali üst üste ekleyerek daha kompleks bir yapıya sahip dalgalar oluşturulabilirdi. 

Örnekle açıklayalım:


Evrim Ağacı’nın kurucusu Dr. Davet Mert Bakırcı, bu durumu üç farklı piyanonun tuşuna birebir anda basmaya benzetiyor. Her biri tuşun sesini birer sinüs dalgalarıyla tabir edebiliyoruz. Bu sesleri üst üste koyduğumuzda ise daha karmaşık bir ses ve ses dalgası elde ediyoruz. 

Fourier, karmaşık dalgaları sinüs dalgalarıyla açıklamak istemişti. Asıl tespiti ise dalgaları birleştirme sürecinin tam zıddını tabir ediyordu.

Karmaşık dalgaların tümünü yüzlerce, binlerce velev milyonlarca kolay dalgaya ayırmak mümkündü!

Yani şayet karmaşık bir sinyal üretmek istiyorsanız, kaç farklı yalın sinyale gereksiniminiz olduğunu hesaplayabilirdik. Bu da ne demek?

Diyelim ki bir müzisyensiniz ve aklınıza hoş bir ezgi geldi...


Bu ezgiyi notalara dökmek, sesleri enstrümanlara dökmek gerekiyor. Yani karmaşık bir ezgiyi daha yalın modüllere ayırmak zorundasınız. Fourier’in Dönüşümü sayesinde gereksiniminiz olan tüm kolay dalgaları hesaplayabilirsiniz. Üstelik doğruluk nispetiniz ise %100 olacaktır.

Fourier’in ürettiği formül karmaşık bir bütünü yalın kesimlere ayırmanın tek adımda gerçekleşmesini sağlıyor. 

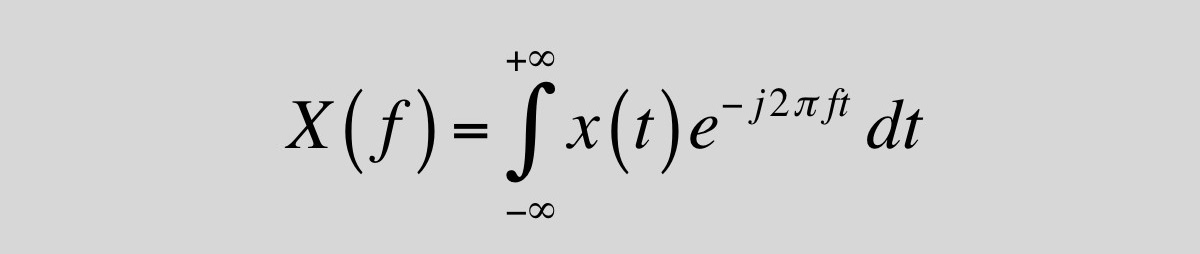
• x(t): Elde etmek istediğiniz karmaşık sinyalin ta kendisi,
• e üzeri (−jπ2ft): Şiddetli görünse de aslında sinüsoid dalgalarını söz ediyor,

İki terimi çarpıp sonucun integralini aldığınızda sinüs dalgalarını olağan kesimlere bölmüş oluyorsunuz. Sonuçtaki X(f) terimi ise her bir yalın sinyal büyüklüğünü ve gecikme ölçüsünü sunuyor.

Artık (nihayet) gelelim günümüze ve bu formülü kullandığımız yanlara:


Aklınıza gelen o hoş ezgiye sahip şarkıyı bestelediniz ve kayda girdiniz. Bütün enstrümanlar teker teker ve başka ayrı çalındı, kaydedildi. Kaydedilen her ses, ülkü bir biçimde üst üste getirildi ve müziğiniz ortaya çıktı. 

Yani birden çokça yalın ses dalgasını üst üste birleştirip karmaşık bir dalgayı, yani şarkıyı oluşturuyorsunuz. 

Yapılması gereken tek bir şey kalıyor: Bu şarkıyı kişilere ulaştırmak ve kolay kolay dinlemelerini sağlamak. İşte o sırada tüm bu karmaşık ses evraklarının tek bir evrakta birleşmesi gerekiyor. Yani 'miksleme' denilen süreci gerçekleştirmeniz lazım. 

Evet, akıllıca bildiniz. .MP3 burada ortaya çıkıyor:


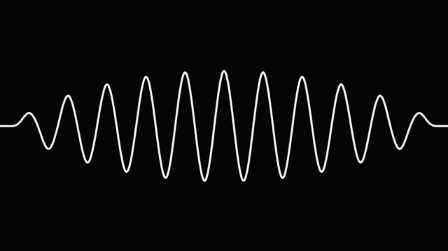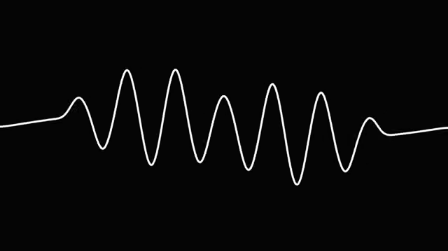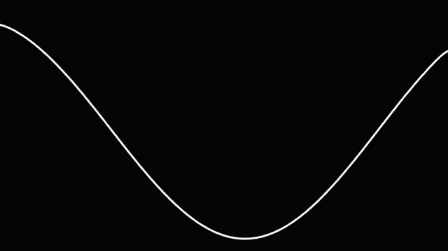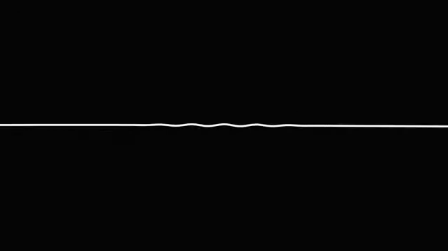
Sıradanda kayıt evraklarını direkt kişilere sunmanız imkansız. Hakikaten ortaya çıkan son belge aktarım etmek için hayli tutarlı bir done boyutuna sahip. 

Şayet dinlediğiniz bir müziği Fourier dönüşümü ile modüllerine ayırırsanız, kimi seslerin düşük ve kimilerinin yüksek frekansa sahip olduklarını görürsünüz. Tanınan evrak formatı .MP3 için de bu durum makbuldür. Bu evrakta duymanın bir mana tabir etmediği tüm gereksiz ses frekansları çıkarılmış olur. Fourier’in dönüşümü sayesinde, yalnızca duymamız gereken sesleri üst üste ekler, sairlerini eleriz. 

Evet, Spotify üzere pratiklerdeki müziklerin .MP3 formatından ne farkı var?


Artık .MP3 üzere tahlillerin de artta kaldığı bir devirdeyiz. Spotify, Shazam ve başka tanınan müzik platformlarındaki belge formatı ise .OGG koduyla bildiğimiz Ogg Vorbis. Bu formattaki dalga dönüşümü ise Fourier Dönüşümü ile değil, Ayrık Kosinüs Dönüşümü ile gerçekleştiriliyor. 

Shazam'da bir müzik arattığınızda tatbik, bu dönüşümü kullanarak ses dalgaları içindeki kolay frakansları ayrıştırıyor. Ayrışan kolay frekanslarla Shazam’ın elindeki olgu tabanında bulunan frekans kıymetleri eşleşince aradığını şarkıyı da bulmuş oluyorsunuz. Yani Shazam, aslında bütün şarkıyı değil, içindeki en müsait frekansları dinleyip ayırt ediyor. 

Gürültü engelleyen kulaklıklar!?


Şayet gerçek bir gürültü engelleyici kulaklığınız varsa kulaklığınız Fourier Dönüşümü’nü kullanıyor. Kulaklık etrafınızdaki sesi algılıyor, kaydediyor, ses spektrumunu yalın dalgalara ayırıyor, tahlil ediyor ve dinlediğiniz müziğin frekanslarını sonuca nazaran değiştiriyor. Tam o sırada yanınızda bir korna çalıyorsa frekanslar yükseliyor ve gürültü anlık olarak kesiliyor.

Görsellerdeki .JPG formatı!?


Yukarıdaki görseli bilgisayarınıza kaydettiğinizde formatı .JPG olacak. Bu kayıt esnasında bilgisayarınız Fourier Dönüşümleri yaparak manzaradaki renkleri ve parlaklıkları olağan dalgalar biçiminde algılayacak ve bazı yüksek frekansları atacak. Atılan bu frekansları biz gözümüzle neredeyse fark bile edemeyeceğiz.

Velev WhatsApp’tan yaptığınız fotoğraf alışverişini düşünün. Olağanda şiddetli büyük piksel içeren o fotoğraflar WhatsApp’tan gidince bir anda görsel kalitelerini kaybediyor. Bu gönderim sırasında WhatsApp pratiği, manzarayı kolay dalgalara ayırıp kimi frekansları siliyor. Sonuç olarak karşı tarafa imaj gidiyor ancak silinen frekanslar yüzünden bariz bir kalite kaybı yaşanıyor. WhatsApp, bu süreçleri aktarımı kolaylaştırmak için gerçekleştiriyor. Sonuç olarak 8-9 MB boyutundaki bir fotoğrafı 150 KB olarak iletebiliyoruz. 

Mükemmel, değil mi?

O vakitler ne yaptığının farkında olmayan Fourier asıl emeline ulaşmış mıydı?

Faurer üzere bir dahi için elbette müziği kolay dinlemek ya da WhatsApp öbeğinden selfie göndermek sorun değildi. Onun ısının iletimiyle ilgilendiğini söylemiştik. Kendisi, ortaya koyduğu dönüşüm formülüyle ısı hareketini modelleyebildi. Isının nasıl iletildiğini çok çok güzel anladı.

Bugün yeryüzünde ya da uzayda bulunan bir araçta kullanılan materyallerin ısıya olan hassaslığını merak ediyorsak tekrar Fourier’in Dönüşümü’ne göz atıyoruz. 

Tek bir formül, 200 yıl içinde işte bu türlü pahalanıyor. 

Umarız bugün öğrendikleriniz; matematik ve umumi olarak tüm ilmî meydanların ne kadar kıymetli olduğunu bir kere daha göstermiştir.

• Menşeler: Evrim Ağacı, Gizmodo